Афинные преобразования.

Парадигма ZenCad предполагает, что большая часть объектов появляется в точке начала координат, после чего перемещается к месту своего назначения с помощью механизма преобразований.

Обычно, при работе с геометрией, преобразования выполняются с помощью методов класса Shape (представляющего геометрические тела), но для построения сложных преобразований или работы с анимацией афинные преобразования также могут создаваться в качестве обособленных объектов.

Афинные преобразования в ZenCad представлены объектами класса Transformation (однородные преобразования) и класса GeneralTransformation (афинное преобразование общего вида). Объекты этих класов порождаются семейством функций описанных ниже в этом разделе.

Следует помнить, что преобразования общего вида вычислительно сложнее и могут сильно изменять внутреннее представление геометрического объекта.

С математической точки зрения объекты преобразования является линейными операторами и относительно них допустимы некоторые операции линейной алгебры. Соответствующий функционал библиотеки описан в разделе "Операции над преобразованиями".

Функции для работы с преобразованиями и специальные виды преобразований описаны в разделе "Дополнительные преобразования".

Базовые преобразования.

Существует четыре базовых преобразования: поворот, трансляция, масштабирование и отражение.

Поворот

Поворот тела вокруг оси заданной вектором v и проходящей через начало координат на угол a.

Если угол a не указан, то в качестве угла поворота берётся радианная мера, численно равная модулю вектора v.

Методы трансформируемых геометрических объектов:

# Основной синтаксис:
shp.rotate([x,y,z], a=None)
shp.rotate(x,y,z)
shp.rotateX(x)
shp.rotateY(y)
shp.rotateZ(z)

# Сокращенный синтаксис:
shp.rot([x,y,z], a=None)
shp.rot(x,y,z)
shp.rotX(x)
shp.rotY(y)
shp.rotZ(z)

Создание объекта трансформации:

rotate([x,y,z], a=None)
rotate(x,y,z)
rotateX(x)
rotateY(y)
rotateZ(z)

Трансляция

Паралельный перенос тела на вектор (x,y,z). По историческим причинам (в частности для совместимости с OpenScad), в библиотеке zencad есть два синонимичных семейства функций/методов translate и move, а также их мнемонические обозначения.

Методы трансформируемых геометрических объектов:

# Основной, альтернативный, мнемонический синтаксис:
shp.translate(x=0,y=0,z=0)
shp.translate([x,y,z])
shp.move(x=0,y=0,z=0)
shp.move([x,y,z])
shp.moveX(x)
shp.moveY(y)
shp.moveZ(z)
shp.right(x) # moveX(+x)
shp.left(x)  # moveX(-x)
shp.forw(y)  # moveY(+y)
shp.back(y)  # moveY(-y)
shp.up(z)    # moveZ(+z)
shp.down(z)  # moveZ(-z)

# Сокращенный синтаксис:
shp.movX(x)
shp.movY(y)
shp.movZ(z)

Создание объекта трансформации:

# Основной синтаксис:
translate(x=0,y=0,z=0)
translate([x,y,z])

# Альтернативный синтаксис:
move(x=0,y=0,z=0)
move([x,y,z])
moveX(x)
moveY(y)
moveZ(z)

# Мнемонический синтаксис:
right(x) # moveX(+x)
left(x)  # moveX(-x)
forw(y)  # moveY(+y)
back(y)  # moveY(-y)
up(z)    # moveZ(+z)
down(z)  # moveZ(-z)

Масштабирование

Изменение размера тела на коэффициент a. Может выполняться в направлении заданной оси или изотропно.

Методы трансформируемых геометрических объектов:

Scaling

Change in body size by coefficient a. It can be performed in the direction of a given axis or isotropic.

Methods for transformable geometric objects:

shp.scale(a)
shp.scaleX(a)
shp.scaleY(a)
shp.scaleZ(a)

Создание объекта трансформации:

scale(a)
scaleX(a) # general_transformation
scaleY(a) # general_transformation
scaleZ(a) # general_transformation
scaleXYZ(x,y,z) # general_transformation

Отражение

Операция отражения геометрии относительно точки, оси проходящей через начало координат или плоскости, проходящей через начало координат.

При отражение относительно точки задаются координаты центра трансформации. При отражение относительно оси задаётся вектор оси трансформации. При отражение относительно плоскости задаётся вектор нормали отражающей плоскости.

Методы трансформируемых геометрических объектов:

# Отражение относительно центра.
shp.mirrorO(x=0,y=0,z=0)
shp.mirrorO([x,y,z])

# Отражение относительно оси.
shp.mirror_axis(x,y,z)
shp.mirror_axis([x,y,z])
shp.mirrorX() # equal to mirror_axis(1,0,0)
shp.mirrorY() # equal to mirror_axis(0,1,0)
shp.mirrorZ() # equal to mirror_axis(0,0,1)

# Отражение относительно плоскости.
shp.mirror_plane(x,y,z)
shp.mirror_plane([x,y,z])
shp.mirrorXY() # equal to mirror_axis(0,0,1)
shp.mirrorYZ() # equal to mirror_axis(1,0,0)
shp.mirrorXZ() # equal to mirror_axis(0,1,0)

Создание объекта трансформации:

# Отражение относительно центра.
mirrorO(x=0,y=0,z=0)
mirrorO([x,y,z])

# Отражение относительно оси.
mirror_axis(x,y,z)
mirror_axis([x,y,z])
mirrorX() # equal to mirror_axis(1,0,0)
mirrorY() # equal to mirror_axis(0,1,0)
mirrorZ() # equal to mirror_axis(0,0,1)

# Отражение относительно плоскости.
mirror_plane(x,y,z)
mirror_plane([x,y,z])
mirrorXY() # equal to mirror_axis(0,0,1)
mirrorYZ() # equal to mirror_axis(1,0,0)
mirrorXZ() # equal to mirror_axis(0,1,0)

Операции над преобразованиями.

Аффинные преобразования являются линейными операторами и относительно них может быть выполнены некоторые операции линейной алгебры.

Композиция.

Композиции аффинных преобразований выполняются с помощью оператора умножения. Следует учесть, что композиции аффинных преобразований некоммутативны.

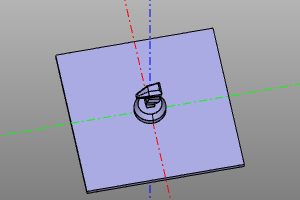
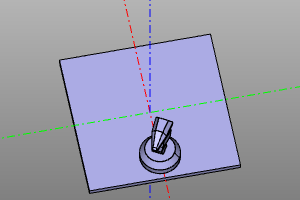
Композиции преобразований следует читать справа налево. Нпример, в примере ниже, запись moveX(20) * rotateZ(deg(60)) Означает, что мы сначала совершаем поворот на 60 градусов, а потом делаем паралельный перенос по оси X на 20 единиц.

Пример:

trans = moveX(20) * rotateZ(deg(60))
m = zencad.internal_models.knight()
disp(trans(m))

# alternate: box(5, center=True).rotZ(deg(60).movX(20)

До	После

Инверсия.

Вычисление обратного преобразования.

Сигнатура:

trsf.inverse()

Пример:

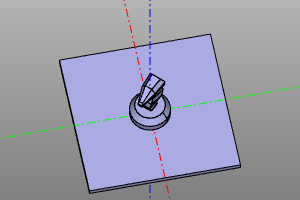
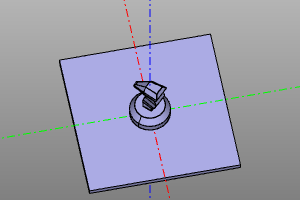
trans = rotateZ(deg(45))
m = zencad.internal_models.knight()
disp(trans(m), color.green)
disp(trans.inverse()(m), color.red)

Преобразование	Инверсия

Пример:

trans = moveX(20) * rotateZ(deg(45))
m = zencad.internal_models.knight()
disp(trans(m), color.green)
disp(trans.inverse()(m), color.red)

Преобразование	Инверсия

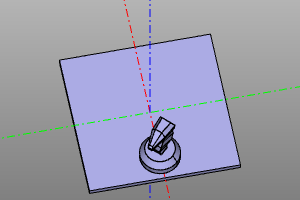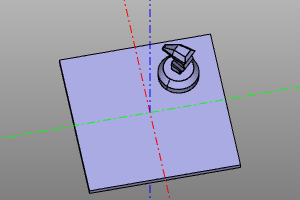Примечание. Инверсия композиции преобразований может быть вычислена как:

(A * B)^-1 = B^-1 * A^-1

Дополнительные преобразования.

Преобразование само в себя.

Специальное преобразование, никак не изменяющее объект.

nulltrans()

До	После

Минимальный поворот.

Данное преобразование соответствует минимальному поворота от вектора f к вектору t.

Сигнатура:

short_rotate(f, t)

Пример:

short_rotate((0,0,1), (1,1,1))(zencad.internal_models.knight())

До	После

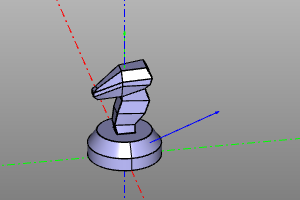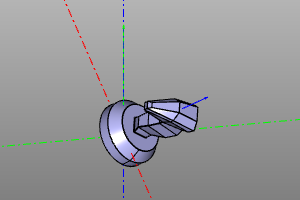Множественное преобразование.

Проводит операцию множественного преобразования прототипа на массив объектов преобразований transes. При этом, если опции array и unit неактивны, производится булево объединение результата. Если активен array, будет возвращен массив результатов. При активации опции unit, будет возвращен сборочный юнит, построенный на массиве результатов.

Операция множественного преобразования может выполняться над интерактивными объектами и сборочными юнитами. В этом случае обыъект преобразования копируется необъходимое число раз. Возврат происходит в виде юнита объединяющего копии или в виде массива при активной опции array. Опция unit при этом ни на что не влияет.

Сигнатура:

multitrans(transes, unit=False, array=False)

Пример:

def extrans(): return multitransform([
translate(-20,20,0) * rotateZ(deg(60)),
translate(-20,-20,0) * rotateZ(deg(120)),
translate(20,20,0) * rotateZ(deg(180)),
nulltrans()
])
disp(extrans(zencad.internal_models.knight()))

До	После

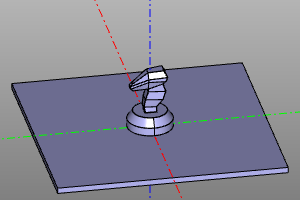Круговой массив.

Множественное преобразование, порождающее круговой массив из n объектов на угловом диапазоне yaw. Параметр endpoint отвечает за включение последней точки линейного пространства углов. (праметры array, unit - см. Множественное преобразование.)

Сигнатура и код преобразования:

def rotate_array(n, yaw=deg(360), endpoint=False, array=False, unit=False):
lspace = np.linspace(0, yaw, num=n, endpoint=endpoint)
transes = [ rotateZ(a) for a in lspace  ]
return multitrans(transes, array=array, unit=unit)

Примеры:

m = zencad.internal_models.knight().move(20,20)
rotate_array(6, yaw=deg(270, endpoint=True)

До	После

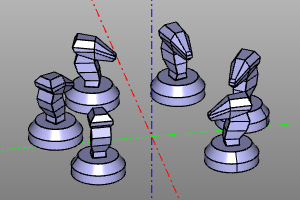Круговой массив c дополнительным креном.

Множественное преобразование, порождающее круговой массив из n объектов на угловом диапазоне yaw. Параметр endpoint отвечает за включение последней точки линейного пространства углов. (праметры array, unit - см. Множественное преобразование.)

Опция roll задаёт интервал крена тела вокруг траектории вращения.

В отличии от rotatearray_ имеет несколько отличную семантику работы с исходным объектом. В rotatearray2_ исходный объект изначально находится в начале координат, после чего разворачивается на 90 градусов вокруг оси X и смещается по оси X на растояние равное радиусу r.

Сигнатура:

rotate_array2(
n, r=None,
yaw=(0,deg(360)), roll=(0,0),
endpoint=False, array=False, unit=False)

Пример:

rotate_array2(
n=60,
r=20,
yaw=(0,deg(270)),
roll=(0,deg(360)),
array=True)(
square(10, center=True, wire=True)
)

До	После

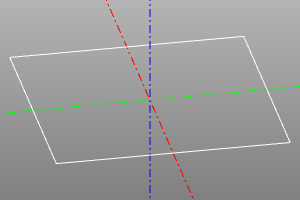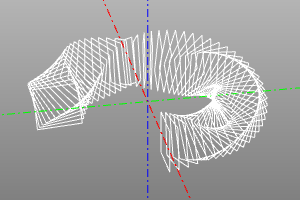Квадратное отражение.

Достраивает 3 отражения исходного объекта.

Сигнатура и код преобразования:

def sqrmirror():
return multitransform([nulltrans(), mirrorYZ(), mirrorXZ(), mirrorZ()])

Пример:

sqrmirror(knight.move(20,30))

До	После