Curve analysis

Theoretical summary.

The generally accepted method for defining curves in computational geometry systems is the parametric method.

According to him, the curve is given by a continuous mapping of the scalar set [U _min, U _max] onto a space of a given dimension. P = F (U): P ∈ R ^ N, U ∈ R ^ 1 [U _min, U _max], where F is the mapping functor and N is the dimension of the space.

In practice, this means that any point P on the curve has a corresponding value of the scalar parameter U. It should be understood that, in the general case, the function connecting the parameter U at the point P and the length of the curve from the start point O to the point P is not linear. Therefore, calculations over a curve in terms of lengths require the use of a special mathematical apparatus (implemented in the form of methods in this library).

Classes of curves.

ZenCad has the following classes that implement curve analysis methods:

• Edge (spawned by segment, interpolate, bezier, bspline, etc.)
• Curve
• Curve2

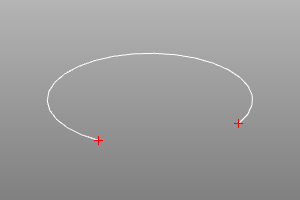
End points and end curve range.

Determines the endpoints of the end curves.

The endpoints method returns endpoint objects. The parameters of these points can be queried using the range method.

curve.endpoints() -> point3, point3
curve.range() -> float, float

crv = circle(r=5, wire=True, angle=deg(270))
s,f = crv.endpoints()
disp([crv, s, f])

curve.length ()

Return the length of the curve between the U \ _min and U \ _max parameters.

curve.d0 (u)

Return the point corresponding to the u parameter.

curve.d1 (u)

Return the vector of the first derivative matching the u parameter.

curve.linoff (u, dist)

Return the parameter of the point offset by the length dist relative to the point specified by the u parameter.

curve.linoff_point (u, dist)

Return the point offset by the length dist relative to the point specified by the u parameter.

curve.project (pnt)

Return the parameter corresponding to the point on the curve closest to the point pnt.

Equidistant curve points.

Return an array of points equally spaced along the curve. The npnts parameter sets the number of points. The parameters umin, umax set the range on the set of parameters in which the distribution procedure will be carried out.

curve.uniform(npnts, umin=U_min, umax=U_max) -> list(float)
curve.uniform_points(npnts, umin=U_min, umax=U_max) -> list(point3)

crv = circle(r=5, wire=True, angle=deg(270))

params = crv.uniform(8, math.pi/4, math.pi)
print(params) # [0.7853981633974483, 1.121997376282069, 1.4585965891666897, 1.7951958020513104, 2.131795014935931, 2.4683942278205517, 2.8049934407051724, 3.141592653589793]

pnts = crv.uniform_points(8, math.pi/4, math.pi)
disp(pnts + [crv])