Triangulation and mesh
EXPERIMENTAL
Functions for working with polygonal representation.
Triangulation
Creation of a polygonal mesh in the format (nodes, triangles), where pnts is an array of points, and triangles is an array of 3-tuples, indices of points. The deflection parameter is responsible for resolving the splitting.
Signature:
nodes, triangles = triangulate(shp, deflection)
Example:
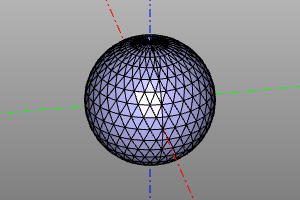
m=sphere(10)
nodes, triangles = triangulate(m, 0.1)
print("count_of_nodes:", len(nodes))
print("count_of_triangles:", len(triangles))
print("first_five_nodes:", nodes[:5])
print("first_five_triangles:", triangles[:5])
#count_of_nodes: 699
#count_of_triangles: 1362
#first_five_nodes: [point3(0.000000,-0.000000,10.000000), point3(0.000000,-0.000000,10.000000), point3(0.000000,-0.000000,-10.000000), point3(1.950903,-0.000000,-9.807853), point3(3.826834,-0.000000,-9.238795)]
#first_five_triangles: [[237, 227, 200], [486, 482, 470], [237, 200, 211], [487, 472, 477], [238, 201, 212]]
Polyhedrone
A solid consisting of flat faces, specified by vertex points pnts and an array of tuples of indices of points defining the faces.
Signature:
polyhedron(pnts, faces, shell=False)
Example:
m=sphere(10)
nodes, triangles = triangulate(m, 0.1)
disp(polyhedron(nodes, triangles))
Convex hull
Construction of the convex hull of a set of points. The scipy.spatial.ConvexHull procedure is used
convexhull_ computes an array of convex hull polygon point indices. convexhullshape builds a convex hull using the polyhedron procedure.
Options: incremental and qhulloptions_ are scipy.spatial.ConvexHull options (see scipy documentation). shell - create a shell instead of a body.
Signature:
convex_hull(pnts, incremental=False, qhull_options=None)
convex_hull_shape(pnts, shell=False, incremental=False, qhull_options=None)
Example:
pnts = points([
( 0, 0, 0),
(10, 0, 0),
(10, 10, 0),
( 0, 10, 0),
( 5, 5, 10),
])
print(convex_hull(pnts))
disp(convex_hull_shape(pnts))